INTRODUCING THE BLOG SERIES
This is the first article in a blog series about introductory quantum mechanics. These articles are mainly based on my notes, which are in turn based on the book Introduction to Quantum Mechanics by David J. Griffiths. It is the book that was used during the Quantum Physics 1 and 2 courses at the University of Groningen when I took these courses.
Before moving on, allow me to make an important disclaimer: I am not a physicist. I am not a mathematician. Nor is Quantum Physics one of my strongest areas. But I do find it fascinating, and I hope that by sharing these notes, you will find it too. I aim to have each of these articles checked by those much more experience in physics (and mathematics).
In these blog series I assume little to no prior physics knowledge. I will try to elaborate on concepts in classical physics as needed, but if there is something you do not understand, don’t be scared to look things up online! A basic knowledge of linear algebra and integral and differential calculus is assumed, however.
Let’s get started then!
ATOMS
Everything around us is made up of atoms, which are very, very tiny objects that are themselves made up of even smaller objects. From the bones in our body to the water we swim in. From the planes we use to go on holiday to the chairs we sit in (for must of us, a bit too much!). The word atom comes from ancient Greek, in which, ironically, it had a meaning that can be translated as indivisible or uncuttable.
All atoms consist of a center, which is referred to as the nucleus, and one or more electrons, ‘orbiting’ around the nucleus. Nuclei are even tinier than atoms themselves: if we consider the nucleus to be an ant inside a soccer stadium, then the electrons would be approximately at the location of the stands. Not all atoms are the same, however. Nuclei consist of smaller objects (particles) which we call protons and neutrons. A more general way to refer to protons and nucleons is by referring to them as neucleons.
We can go even further. In fact, protons and neutrons are in turn made up of quarks, even tinier particles. Although not quite relevant to the course, you may be interested in knowing that nucleons owe their charge to their quark contents. Protons, for example, are made up of two up-type quarks and one down-type quark, which have charges \(+\dfrac{2}{3}e\) and \(-\dfrac{1}{3}e\) respectively. This means that \(\dfrac{2}{3}e+\dfrac{2}{3}e-\dfrac{1}{3}e=1e\), which is precisely the charge of a proton.
A popular approach to visualizing atoms is to draw them as satellites orbiting a planet, as in the image below.

However, as you will read later in this post, a slightly more accurate representation would be the following:

The lightest atom is the hydrogen-1 atom, which consists of just a single proton and a single electron. One of the heaviest elements is uranium, which has 92 protons. The number of neutrons may vary. Each version of a specific atom (i.e., a different number of neutrons) is known as an isotope. For example, a hydrogen atom with one neutron is known as hydrogen-2 or deuterium. A future course on nuclear physics will cover these more extensively, for now we will just focus on hydrogen-1, since it makes our calculations a lot easier.
CLASSICAL MECHANICS, QUANTUM MECHANICS AND RELATIVITY
The field of quantum mechanics describes the dynamics of things at an incredibly small scales: at the scale of molecules, atoms and smaller. Physicists found that, at this level, the laws of classical mechanics no longer seem sufficient. The transition from classical mechanics is governed by a single fundamental constant \(\hbar\) (the reduced Planck constant).
In a similar fashion we have the extension of special relativity, which is governed by \(c\), the speed of light. Special relativity allows for relativistic effects to be taken into account, which occur when objects travel at very large speeds.
A field referred to as quantum field theory includes both relativistic and quantum effects. Consider the standard model of elementary particles, which covers particles such as electrons. The term elementary refers to the fact that these particles are considered to be unbreakable: they are not made up of smaller particles. Hence, one would not find protons in the standard model but rather its constituent quarks, \(u\) and \(d\).
The diagram below displays the relation between these theories.
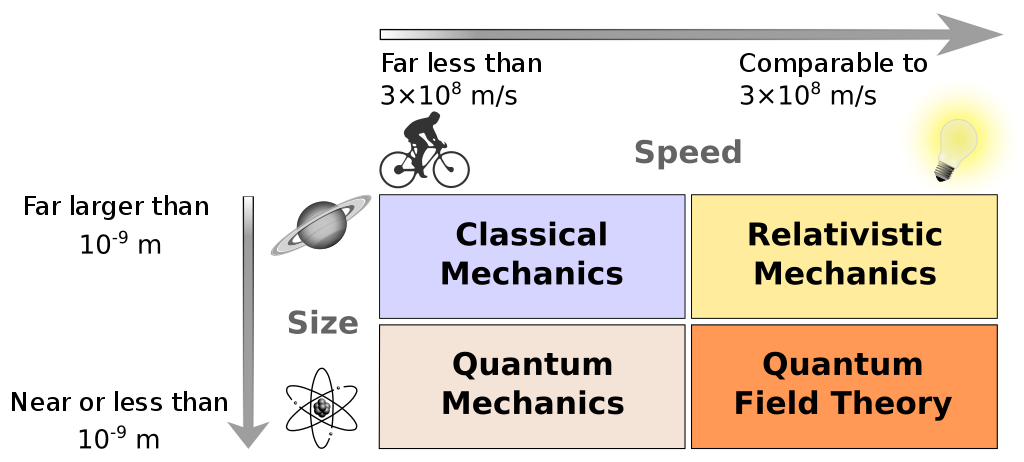
The third extension is gravity, governed by the gravitational constant \(g\). Combining gravity and special relativity results in the theory called general relativity.
A unified theory considering relativistic, quantum and gravitational effects is referred to as quantum gravity. Two popular theories are string theory and loop quantum gravity. Yet, at the time of writing these theories are still very poorly understood.
In this course we will focus on non-relativistic quantum mechanics.
THE WAVE FUNCTION
Imagine a tennis ball in one-dimensional space (for simplicity we will assume the one-dimensional case for the time being, i.e., assuming that the ball can only move left or right). Due to the tennis ball being big enough, we can describe it using the laws of classical mechanics. These laws tells us that the position of the particle at a time \(x\) is given by \(x(t)\) and its velocity is given by \(\dfrac{dx}{dt}\). Seems simple enough, right?
Now let us shrink the tennis ball down in size, such that it reaches the size of an electron inside an atom.
At this level, objects (particles) are no longer described by these functions but instead by a wave function \(\Psi(\vec{r}, t)\), which is obtained by solving the Schrödinger equation, which in the one-dimensional case has the following shape:
$$i\hbar\dfrac{\partial^2\Psi}{\partial t^2} = \dfrac{\hbar^2}{2m}\dfrac{\partial^2\Psi}{\partial x^2}+V\Psi$$
Rather than giving a specific position of a particle, the wave function gives the probability that the particle can be found at a certain point. We can use the wave function for other things as well, such as calculating the momentum of a particle.
The Schrödinger equation looks intimidating, so let us decompose it. It simply tells us how the wave function of a particle evolves over time. Notice that it is a partial differential equation with both a spatial and temporal dependence. Also notice that it is a complex function, due to the imaginary component \(i\) (the square root of \(-1\)). Does that mean that the results of a quantum mechanical calculation will be imaginary? No, not at all. The wave function itself will be imaginary, however this imaginary component drops out once we attempt to calculate, for example, the position (you will see why later).
The \(\hbar\) is known as the reduced Planck constant. It can be seen everywhere in quantum mechanics, and can be thought of as some sort of conversion number that governs the transition from classical to quantum mechanics. It’s value is the normal Planck constant divided by \(2\pi\):
$$\hbar = \dfrac{h}{2\pi} = 1.054572 \cdot 10^{-34} J\cdot s$$
The remaining coefficient in the left sign of the equality operator is a second-order spatial derivative. On the right hand side we see the Hamiltonian operator acting on the wave function \(\Psi\). We will discuss operators a lot more later, but for now let us just say that the Hamiltonian operator gives us the total energy of the particle. In quantum mechanics, the Hamiltonian represents the same thing as in classical mechanics: the sum of the kinetic and potential energies.
If you have not studied classical mechanics before, imagine a tennis ball on the edge of a high cliff. While it is stationary, it has an incredible amount of potential energy. As the ball gets pushed off the cliff, it gains kinetic energy. The total energy is the same however: as the ball gains kinetic energy, it loses potential energy.
For simplicity we will assume a conservative system. What that means is that we consider the potential energy to be constant, i.e., independent of time. A temporal dependence may be more interesting if we are, for example, dealing with electric fields that change over time.
Solving the Schrödinger equation gives us the wave equation. Over the course of the blog series we will actually try to solve the equation.
SOME FINAL THOUGHTS
In the next few posts we go into much more detail on the concept of a wave function in quantum mechanics. For now let us end this post with some final thoughts.
Quantum mechanics is inherently probabilistic. In classical mechanics we know where an object will be at any time \(t\) if we know its trajectory. In quantum mechanics we do not know exactly where the object is. We just know where it is most likely to be. This probability distribution is given by the wave function. This is one of the most fundamental concepts of quantum mechanics. And it is also one of the hardest concepts to truly accept.
EXERCISES
- What is an isotope?
- Why are particles such as protons and neutrons not part of the standard model, while particles such as electrons are in the standard model?
- What is the difference between the Planck constant \(h\) and the reduced Planck constant \(\hbar\)?
REFERENCES
- Griffiths, D.J. and Schroeter, D.F., 2018. Introduction to quantum mechanics. Cambridge university press.
- De Sanctis, E., Monti, S. and Ripani, M., 2016. Energy from nuclear fission. Undergraduate Lecture,© Springer International Publishing Switzerland.